机械臂说明与 D-H 参数

ZJU-I 型桌面机械臂为典型的六自由度机械臂。一个机械臂运行的视频：

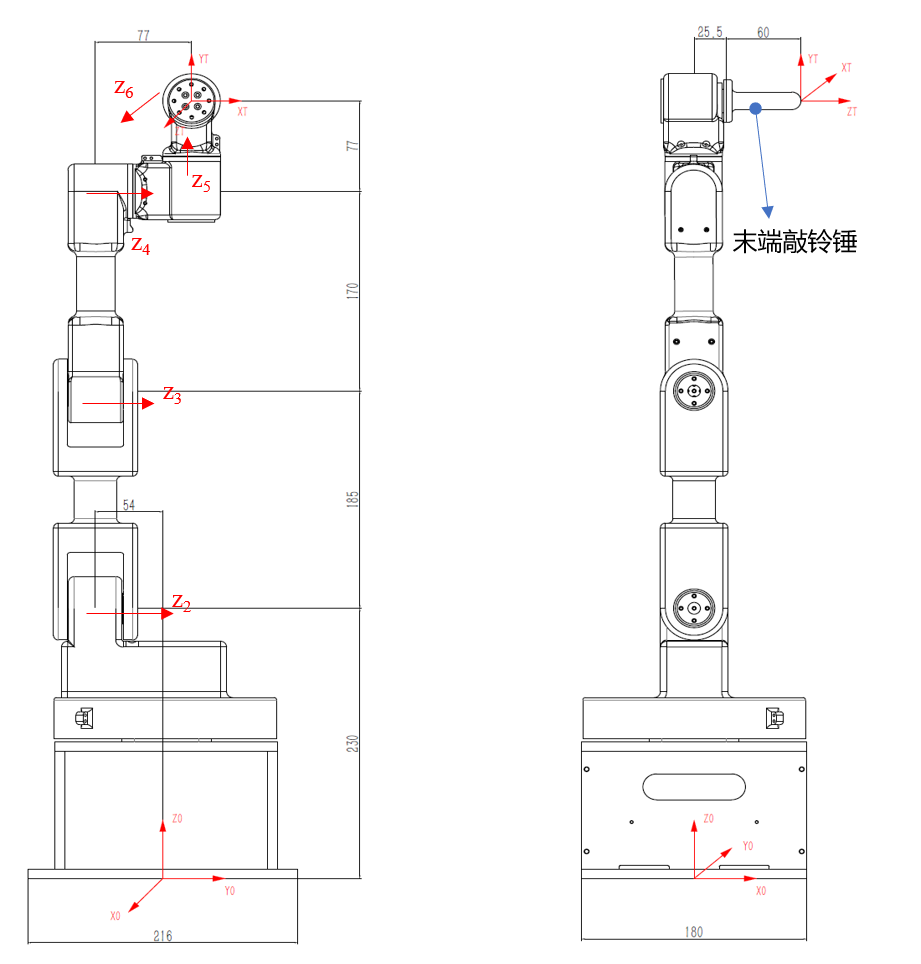
关节角限制为：

坐标系有多种选取方式。机械臂的 D-H 参数的一种表示为：

求解变换矩阵

显然，手算求解机械臂的变换矩阵非常困难。

我们利用 Mathematica 强大的符号计算功能帮助我们运算，代码为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

ConvertDh[dh_] :=
    (
        len = Length[dh];
        h = Table[0, {i, len}];
        For[i = 1, i <= len, i++,
            h[[i]] = ({{Cos[dh[[i, 4]]], -Sin[dh[[i, 4]]], 0, dh[[i, 
                2]]}, {Sin[dh[[i, 4]]] * Cos[dh[[i, 1]]], Cos[dh[[i, 4]]] * Cos[dh[[i,
                 1]]], -Sin[dh[[i, 1]]], -Sin[dh[[i, 1]]] * dh[[i, 3]]}, {Sin[dh[[i, 
                4]]] * Sin[dh[[i, 1]]], Cos[dh[[i, 4]]] * Sin[dh[[i, 1]]], Cos[dh[[i,
                 1]]], Cos[dh[[i, 1]]] * dh[[i, 3]]}, {0, 0, 0, 1}})
        ];
        T = h[[1]];
        For[i = 2, i <= len, i++,
            T = T . h[[i]]
        ];
        FullSimplify[T]
    );

求出变换矩阵为：

$$ \left[\begin{array}{cccc} -c_6\left(c_5 s_1+c_1 c_{234} s_5\right)+c_1 s_{234} s_6 & c_5 s_1 s_6+c_1\left(c_6 s_{234}+c_{234} s_5 s_6\right) & c_1 c_{234} c_5-s_1 s_5 & c_1\left(0.0855 c_{234} c_5+0.185 s_2+0.17 s_{23}+0.077 s_{234}\right)+s_1\left(-0.023-0.0855 s_5\right) \\ c_1 c_5 c_6+s_1\left(-c_{234} c_6 s_5+s_{234} s_6\right) & c_6 s_1 s_{234}+\left(-c_1 c_5+c_{234} s_1 s_5\right) s_6 & c_{234} c_5 s_1+c_1 s_5 & s_1\left(0.0855 c_{234} c_5+0.185 s_2+0.17 s_{23}+0.077 s_{234}\right)+c_1\left(0.023+0.0855 s_5\right) \\ c_6 s_{234} s_5+c_{234} s_6 & c_{234} c_6-s_{234} s_5 s_6 & -c_5 s_{234} & 0.23+0.185 c_2+0.17 c_{23}+0.077 c_{234}-0.0855 c_5 s_{234} \\ 0 & 0 & 0 & 1 \end{array}\right] $$

写得方便看一点：

$$ \begin{aligned} t_{11} &= -c_{6}\left(c_{5} s_{1}+c_{1} c_{234} s_{5}\right)+c_{1} s_{234} s_{6} \\ t_{12} &= c_{5} s_{1} s_{6}+c_{1}\left(c_{6} s_{234}+c_{234} s_{5} s_{6}\right) \\ t_{13} &= c_{1} c_{234} c_{5}-s_{1} s_{5} \\ t_{14} &= c_{1}\left(0.0855 c_{234} c_{5}+0.185 s_{2}+0.17 s_{23}+0.077 s_{234}\right)+s_{1}\left(-0.023-0.0855 s_{5}\right) \\ t_{21} &= c_{1} c_{5} c_{6}+s_{1}\left(-c_{234} c_{6} s_{5}+s_{234} s_{6}\right) \\ t_{22} &= c_{6} s_{1} s_{234}+\left(-c_{1} c_{5}+c_{234} s_{1} s_{5}\right) s_{6} \\ t_{23} &= c_{234} c_{5} s_{1}+c_{1} s_{5} \\ t_{24} &= s_{1}\left(0.0855 c_{234} c_{5}+0.185 s_{2}+0.17 s_{23}+0.077 s_{234}\right)+c_{1}\left(0.023+0.0855 s_{5}\right) \\ t_{31} &= c_{6} s_{234} s_{5}+c_{234} s_{6} \\ t_{32} &= c_{234} c_{6}-s_{234} s_{5} s_{6} \\ t_{33} &= -c_{5} s_{234} \\ t_{34} &= 0.23+0.185 c_{2}+0.17 c_{23}+0.077 c_{234}-0.0855 c_{5} s_{234} \\ t_{41} &= 0 \\ t_{42} &= 0 \\ t_{43} &= 0 \\ t_{44} &= 1 \end{aligned} $$

正运动学

我们完成了 ForwardKinematicsZJU 函数，输入关节角，得到末端空间位置和 XYZ 欧拉角。由于代码太长，这里不做展示，可在文末链接查看。

例如：

In[=] := Import[FileNameJoin[{NotebookDirectory[], "zjui.wl"}]](*导入 zjui.wl*)

In[=] := ForwardKinematicsZJU[{Pi/6, 0, Pi/6, 0, Pi/3, 0}]
In[=] := {0.0904941, 0.164305, 0.607533, -1.82391, -0.0580453, -2.69295}

逆运动学

我们完成了 BackwardKinematicsZJU 函数，输入末端空间位置和 XYZ 欧拉角，得到 6 个关节角。（可能输出多组解，已考虑关节角限制）

例如：

In[=] := Import[FileNameJoin[{NotebookDirectory[], "zjui.wl"}]](*导入 zjui.wl*)

In[=] := BackwardKinematicsZJU[{0.117, 0.334, 0.499, -2.019, -0.058, -2.190}]
In[=] := {{1.04692, 0.543234, 0.531454, -0.551512, 0.523909, 0.698541}, {1.04692, 1.05169, -0.531454, 0.00294118, 0.523909, 0.698541}}

开源链接

Github 开源仓库：ZJUI-Arm-Kinematics

参考资料

六轴UR机械臂标准DH正逆运动学公式推导+代码验证C++ 作者：FuYongqing0412

如果不知道如何安装 Mathmetica，可以参考：Mathematica 激活指南

致谢

感谢 DX3906G 同学提供的逆运动学运算步骤。